이진트리 구현과 순회
이진트리란, 노드(== 버택스)로 구성된 비선형적이고 계층적인 자료구조이다. 각각의 노드는 부모 노드로서 0개 이상 2개 이하의 자식 노드를 가지고 있으며 간선(Edge)로 연결된다. 자식 노드는 각각 왼쪽, 오른쪽 자식노드로 구분되고, 부모가 같은 노드들은 형제 노드라고 한다. -> 자식의 갯수를 최대 2개까지로 제한하기 때문에 이진트리라고 불린다.
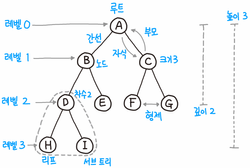
C#을 통해 위 이미지의 트리구조를 구현한다면 아래와 같다.
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace _230209_1
{
class Tree
{
Node root;
public Tree()
{
Node nI = new Node('I', null, null);
Node nH = new Node('H', null, null);
Node nG = new Node('G', null, null);
Node nF = new Node('F', null, null);
Node nE = new Node('E', null, null);
Node nD = new Node('D', nH, nI);
Node nC = new Node('C', nF, nG);
Node nB = new Node('B', nD, nE);
Node nA = new Node('A', nB, nC);
this.root = nA;
}
}
class Node
{
char name;
Node left;
Node right;
public Node(char name, Node left, Node right)
{
this.name = name;
this.left = left;
this.right = right;
}
}
}
- Node 클래스에서는 Node 클래스의 인스턴스가 생성될 때 자식 노드의 정보와 자신의 정보를 저장할 수 있도록 구성되어있다. 현재는 위 이미지의 노드가 문자형 글자(이름) 만을 정보로 가지고 있기 때문에 char형 name변수에 노드의 정보를 저장하지만 노드가 이름외에 다른 정보를 가지고 있다면 딕셔너리를 사용하여 정보를 저장할 수 있다.
- Tree 클래스에서는 노드들을 인스턴스화 하면서 Tree 클래스가 루트 노드의 값을 알도록 구성하였다.
위와 같은 이진트리는 계층성이 있는 정보를 저장하거나 구성할 때, 단순 배열을 통해 정보를 저장하는 것보다 검색/탐색시간을 줄일 수 있다는 장점이 있다. (정보가 계층성이 없어 트리가 일방향적(한 쪽으로 치우치면)으로 구성되면 장점이 사라짐) C#에서 이진트리의 검색은 재귀함수를 통하여 구현할 수 있다.
1. 전위순회 (Pre-Order)
루트 노드부터 왼쪽 자식노드를 계속해서 방문하며 탐색하고 왼쪽자식 노드가 없을 때(Null일 때) 그 형제 노드를 탐색하도록 순회하며 이진트리를 검색하는 방법이다.

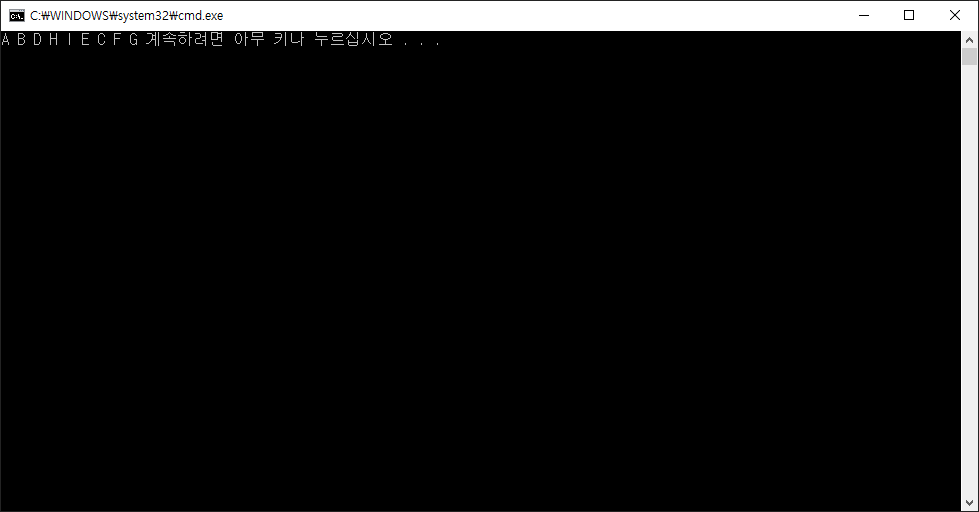
그렇기 때문에 순회 순서는 A - B - D - H - I - E - C - F - G 가 된다. 이를 C#에서 구현한다면 아래와 같다.
class Tree
{
Node root;
public Tree()
{
Node nI = new Node('I', null, null);
Node nH = new Node('H', null, null);
Node nG = new Node('G', null, null);
Node nF = new Node('F', null, null);
Node nE = new Node('E', null, null);
Node nD = new Node('D', nH, nI);
Node nC = new Node('C', nF, nG);
Node nB = new Node('B', nD, nE);
Node nA = new Node('A', nB, nC);
this.root = nA;
this.Preorder(this.root);
}
private void Preorder(Node node)
{
if (node != null)
{
Console.Write("{0} ", node.name);
Preorder(node.left);
Preorder(node.right);
}
}
}
2. 중위순회 (In-Order)
루트 노드부터 왼쪽 자식 노드를 방문한다. 만약 방문한 노드의 자식이 없다면 해당 노드를 탐색한 후 부모노드를 방문하고 탐색한 후 해당 부모노드의 오른쪽 자식 노드를 탐색한다. (가장 왼쪽 자식 노드를 가장 먼저 탐색하고 거슬러 올라가 노드를 2번째 방문하면 것이라면 탐색한 후 오른쪽 자식 노드를 탐색하는 방식)

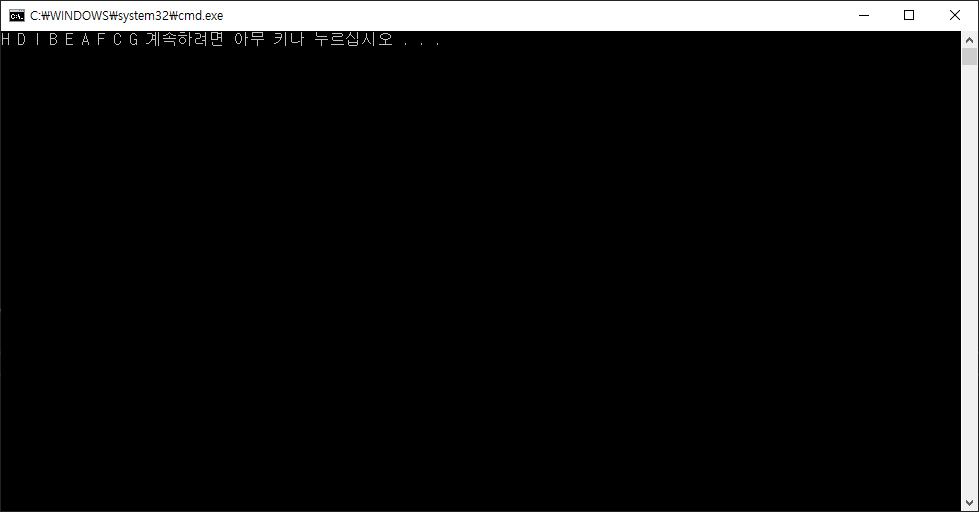
방문 순서는 H - D - I - B - E - A - F - C - G 이다
class Tree
{
Node root;
public Tree()
{
Node nI = new Node('I', null, null);
Node nH = new Node('H', null, null);
Node nG = new Node('G', null, null);
Node nF = new Node('F', null, null);
Node nE = new Node('E', null, null);
Node nD = new Node('D', nH, nI);
Node nC = new Node('C', nF, nG);
Node nB = new Node('B', nD, nE);
Node nA = new Node('A', nB, nC);
this.root = nA;
this.Inorder(this.root);
}
private void Inorder(Node node)
{
if (node != null)
{
Inorder(node.left);
Console.Write("{0} ", node.name);
Inorder(node.right);
}
}
}
3. 후위순회 (Post-Order)
루트 노드부터 왼쪽으로 방문을 시작하여 더 이상 자식노드가 없을 때 해당 노드를 탐색하고 해당 노드가 형제 노드가 있을 때 형제 노드를 탐색한 후 부모노드를 탐색한다. (방문한 노드의 자식 노드 중 더 이상 방문할 자식 노드가 없을 때 해당 노드를 탐색하는 방식)

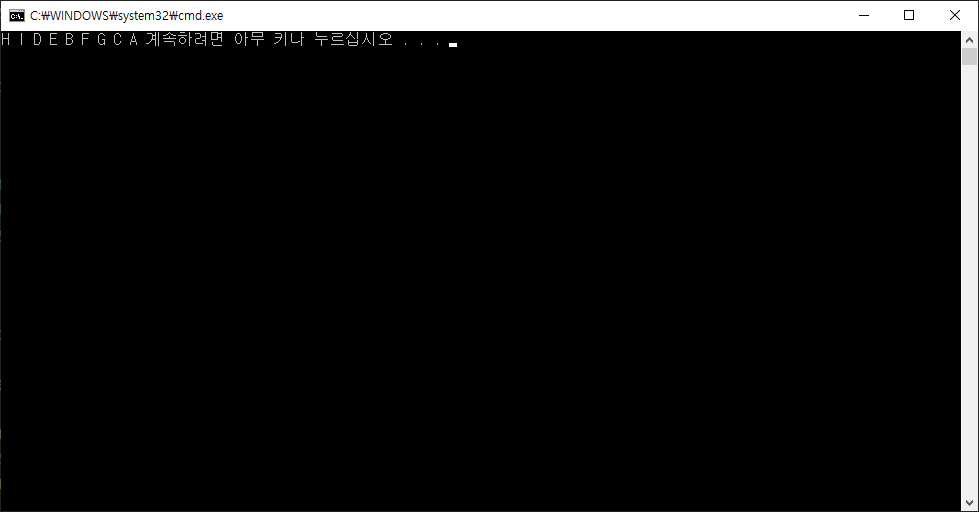
방문 순서는 H - I - D - E - B - F - G - C - A 이다.
class Tree
{
Node root;
public Tree()
{
Node nI = new Node('I', null, null);
Node nH = new Node('H', null, null);
Node nG = new Node('G', null, null);
Node nF = new Node('F', null, null);
Node nE = new Node('E', null, null);
Node nD = new Node('D', nH, nI);
Node nC = new Node('C', nF, nG);
Node nB = new Node('B', nD, nE);
Node nA = new Node('A', nB, nC);
this.root = nA;
this.Postoreder(this.root);
}
private void Postoreder(Node node)
{
if(node != null)
{
Postoreder(node.left);
Postoreder(node.right);
Console.Write("{0} ", node.name);
}
}
}
트리의 탐색을 스택이나 큐배열로 진행할 때는 구조적 이해가 쉽지만 같은 원리의 재귀함수를 사용했을 때는 구조 이해가 쉽지 않다. 자주 사용하면서 원하는 상황에 원하는 탐색 방법을 떠올릴 수 있는 것이 중요하다.