C#) 다익스트라(Dijkstra) 알고리즘

다익스트라(Dijkstra) 알고리즘이란?

 

  그래프의 한 정점(노드)에서 다른 정점까지의 최단 경로를 구하는 알고리즘으로 첫 번째 정점에서 목표 정점까지 존재하는 모든 정점을 방문하여 목표정점까지 최단 거리를 구한다. 아래 이미지를 활용하여 다익스트라 알고리즘에 대해 쉽게 이해할 수 있다. 

 

나무위키

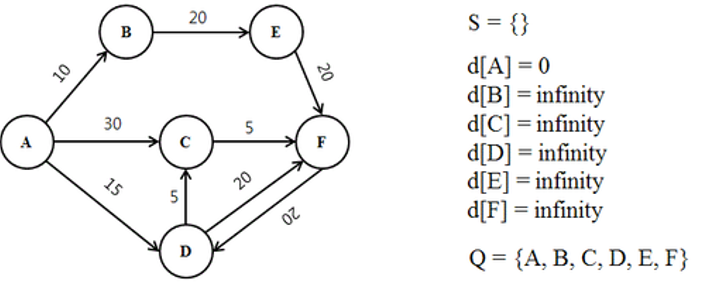
  위 이미지의 A정점에서 B정점까지 도달하는 최단거리는 10이다. 그렇다면 A정점에서 C정점까지 도달할 수 있는 최단 거리는 30일까? 그렇지 않다. C가지 도달할 수 있는 경우의 수를 따져본다면, A에서 C로 바로 가는 방법도 있지만 A에서 D를 방문하여 거리를 탐색하고 C를 방문할 수도있다. 후자의 경우 경로의 길이는 20으로 30보다 짧은 거리인 것을 알 수 있다. 이런 식으로 출발 정점에서 목표한 정점까지 연결된 모든 정점들을 방문하여 도달가능한 모든 경우의 수를 탐색하고 최단 경로를 구하는 알고리즘이 다익스트라 알고리즘이다.

 

 

구현 방식

 

 위 이미지의 A정점에서 F정점까지의 최단경로를 다익스트라 알고리즘을 통해 찾는다면 아래와 같다.

 

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;

namespace Dijkstra
{
    class Program
    {
        public enum eNode
        {
            A, B, C, D, E, F
        }

        static void Main(string[] args)
        {
            Graph graph = new Graph(6);

            graph.AddEdge((int)eNode.A, (int)eNode.B, 10);
            graph.AddEdge((int)eNode.A, (int)eNode.D, 15);
            graph.AddEdge((int)eNode.A, (int)eNode.C, 30);

            graph.AddEdge((int)eNode.B, (int)eNode.E, 20);

            graph.AddEdge((int)eNode.C, (int)eNode.F, 5);

            graph.AddEdge((int)eNode.D, (int)eNode.C, 5);
            graph.AddEdge((int)eNode.D, (int)eNode.F, 20);

            graph.AddEdge((int)eNode.E, (int)eNode.F, 20);

            graph.AddEdge((int)eNode.F, (int)eNode.D, 20);

            List<int> shortestPath = graph.Dijkstra((int)eNode.A, 5);

            foreach(int node in shortestPath)
            {
                Console.Write("{0} ", (eNode)node);
            }
        }
    }

    class Graph
    {
        private int[,] adj;
        private int size;
        List<int> path = new List<int>();

        public Graph(int size)
        {
            this.size = size;
            this.adj = new int[this.size, this.size];
        }

        public void AddEdge(int a, int b, int dist)
        {
            this.adj[a, b] = dist;
        }

        public List<int> Dijkstra(int start, int dest)
        {
            bool[] visited = new bool[this.size];
            int[] distance = new int[this.size];
            int[] parent = new int[this.size];

            for(int i = 0; i < distance.Length; i++)
            {
                distance[i] = Int32.MaxValue;
            }

            distance[start] = 0;
            parent[start] = start;

            while (true)
            {
                int now = -1;
                int closest = Int32.MaxValue;
                for(int i = 0; i < this.size; i++)
                {
                    if (visited[i]) continue;

                    if (distance[i] == Int32.MaxValue) continue;

                    if(distance[i] < closest)
                    {
                        closest = distance[i];
                        now = i;
                    }
                }

                if (now == -1) break;

                visited[now] = true;

                for(int next = 0; next < this.size; next++)
                {
                    if (this.adj[now, next] == 0) continue;

                    if (visited[next]) continue;

                    int nextDist = distance[now] + this.adj[now, next];

                    if(nextDist < distance[next])
                    {
                        distance[next] = nextDist;
                        parent[next] = now;
                    }
                }
            }

            return this.CalcPathFromParent(parent, dest);
        }

        private List<int> CalcPathFromParent(int[] parent, int dest)
        {
            Console.WriteLine("{0}까지 최단 경로 : ", dest);
            while(parent[dest] != dest)
            {
                this.path.Add(dest);
                dest = parent[dest];
            }

            this.path.Add(dest);
            this.path.Reverse();

            return this.path;
        }
    }
}